You will have to screen-print and re-post what you want us to look at. You appear to have the luxury of sitting behind a fully paid-up subscription service, as your links give us a login screen, whereas us mortals have to try to figure stuff out for ourselves and use critical thinking to guide us.
So let us use critical thinking (or is 'education' these days only about some spoon-feeding?).
The equation for electrostatics is F=Q1.Q2/[4.pi.eo.r^2]. If we integrate, wrt r, from infinity to some distance r for two unit charges we get E=~2E-28J.m, or 1.5E-9eV.m. So for a potential of 40MeV this would imply a distance of 1.5E-9/40E6 = 0.04 fm, which appears to be smaller than that quoted for the diameter of nucleii. Whereas your figure of 480 keV implies a distance to the potential peak of 3 fm, which seems more in order.
So I am happy to anticipate adjusting my understanding of this, subject to the answer to a few more points, and
withdraw my statement, as you quoted above, on hold pending correction and to establish if I have been mislead by such texts as I linked to....
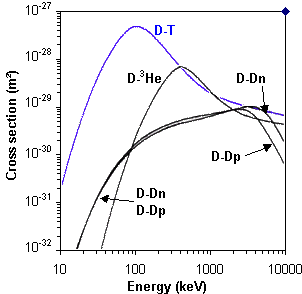
However, this calculation of the Coulomb barrier cannot be the whole picture, or even half of it, because if we look at the fusion cross-section of DT then it peaks as 64 keV ,and the cross-section keeps going on downwards from there on to 480 keV and beyond. This is similar for DD which peaks around 1.1 MeV. Further, the cross-section for pp isn't the same as that of DD and DT, so what we are looking at is a wholly dissimilar set of 'responses' of unit charges in the range close to the nucleus, and it doesn't seem to be the case that there is some unique point at which the Coulomb barrier is overcome, as per the nugget of the point in this thread.
As I look at the fusion cross-section curve and your statement that the Coulomb barrier is at 480 keV, I see nothing particularly noteworthy to suggest that there are two 'competing' forces here either side of that potential.
That the reactivity of DD and DT drops for energies
above the suggested Coulomb barrier, then the logic seems flawed somewhere and doesn't look like it adds up.
So, before throwing around 'absolutes' as quoted from someone's favourite physics texts, I would want to ask a few more questions. As I work far from the physics sector and have no-one knowledgeable to ask questions of, then I would suggest, WizWom, that you could go discuss this with the people you work/study with and figure this out:
Assuming the range at which the strong force dominates over the Coulomb force is a fm or two, why do fusion reactivity cross-sections drop off above the Coulomb barrier energy that this range infers?
WizWom wrote:There is no reasonable Fe+n or Fe+d reaction that gives n, barring amazingly high energies.
Dealt with.